Start / LessWrong (30+ Karma) / Compressed computation is probably not computation in superposition by jai bhagat sara molas medina giorgi giglemiani stefanhex

LessWrong (30+ Karma)

“Compressed Computation is (probably) not Computation in Superposition” by Jai Bhagat, Sara Molas Medina, Giorgi Giglemiani, StefanHex

22 min • 23 juni 2025

Audio note: this article contains 113 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.

This research was completed during the Mentorship for Alignment Research Students (MARS 2.0) Supervised Program for Alignment Research (SPAR spring 2025) programs. The team was supervised by Stefan (Apollo Research). Jai and Sara were the primary contributors, Stefan contributed ideas, ran final experiments and helped writing the post. Giorgi contributed in the early phases of the project. All results can be replicated using this codebase.

Summary

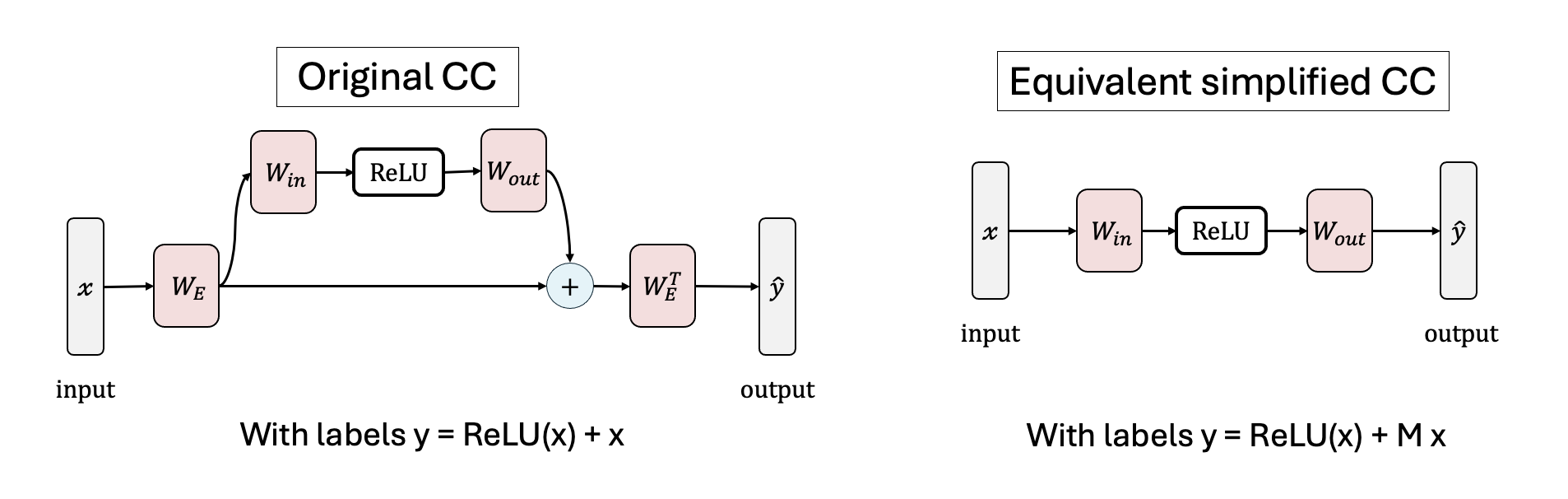
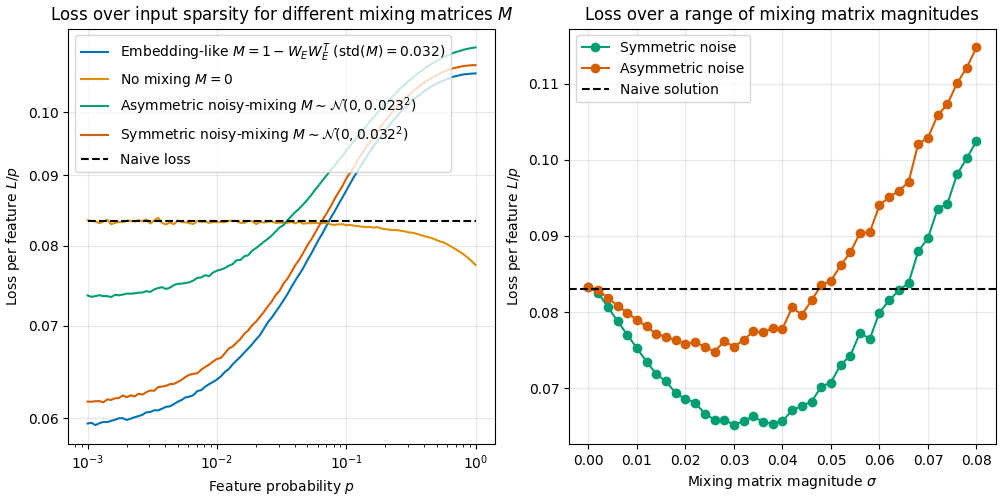
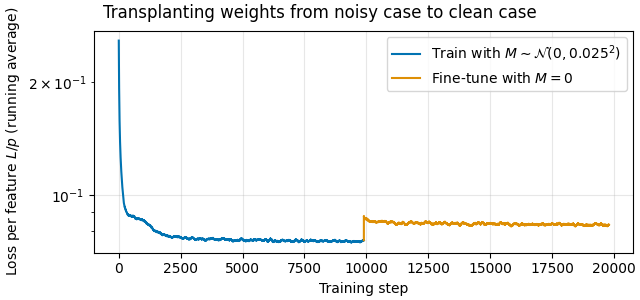
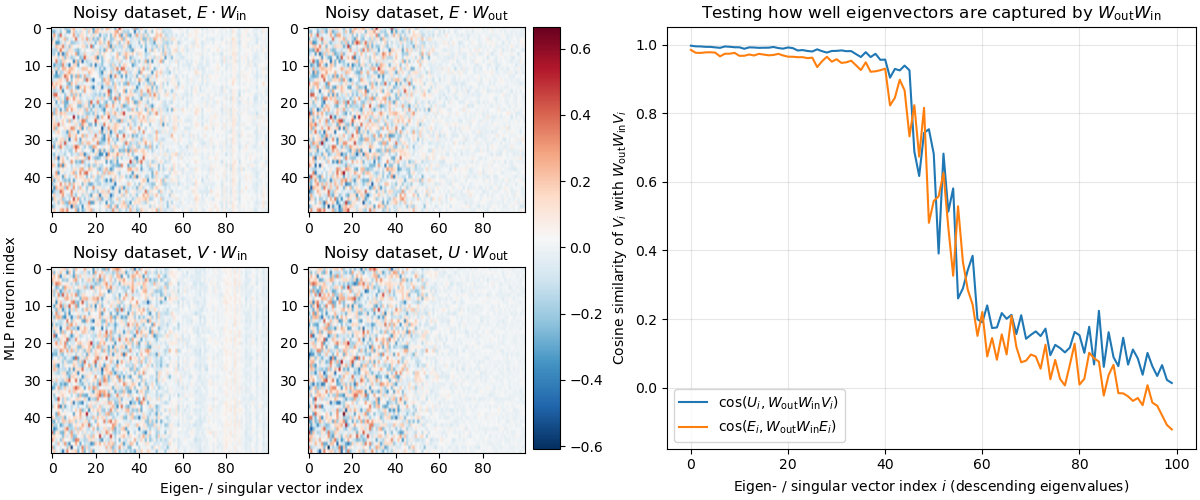
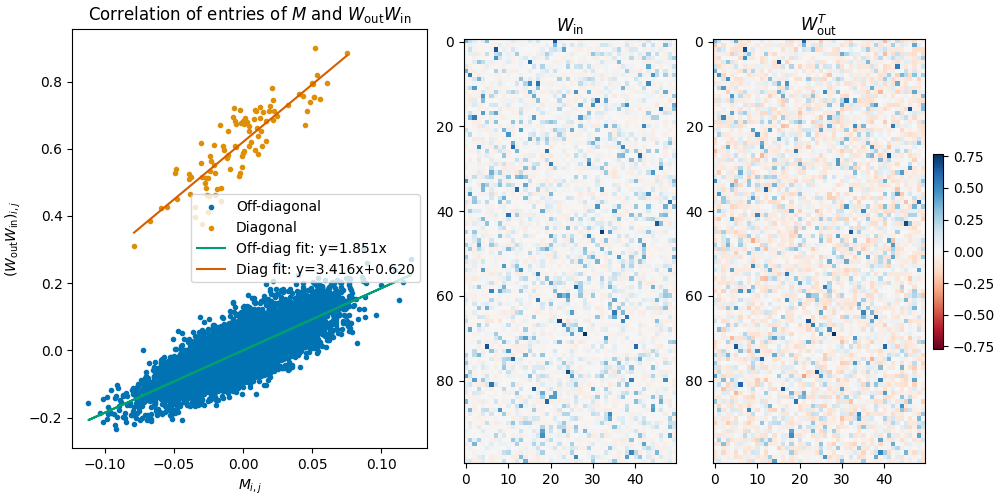
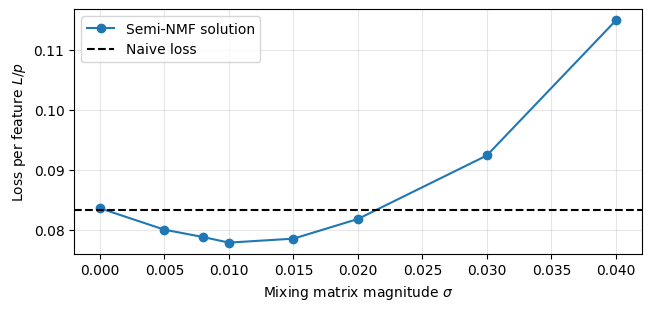
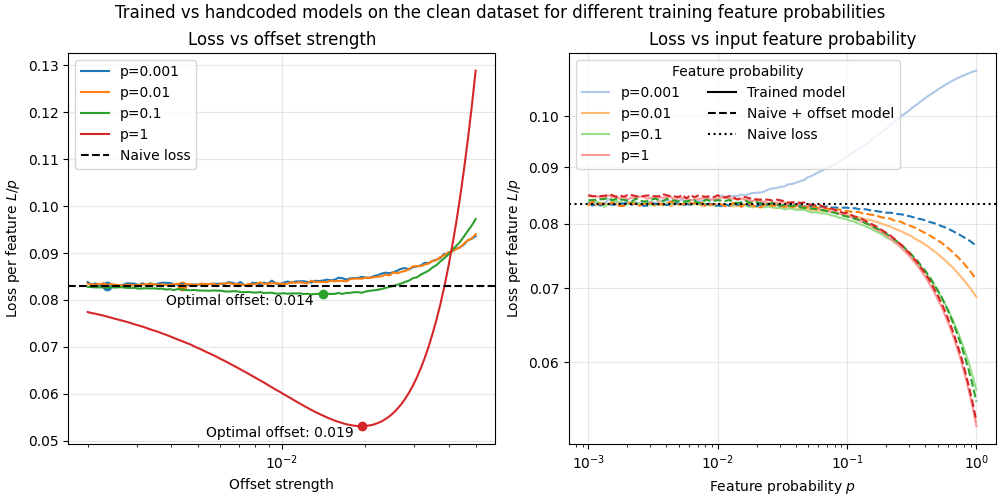
We investigate the toy model of Compressed Computation (CC), introduced by Braun et al. (2025), which is a model that seemingly computes more non-linear functions (100 target ReLU functions) than it has ReLU neurons (50). Our results cast doubt on whether the mechanism behind this toy model is indeed computing more functions [...]

---

Outline:

(00:59) Summary

(02:42) Introduction

(04:38) Methods

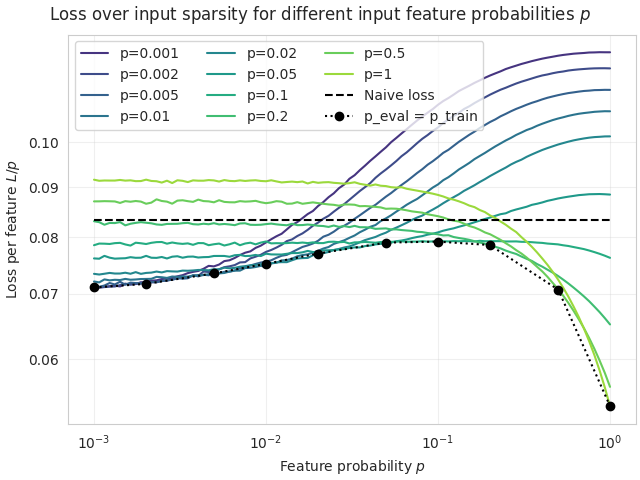
(06:34) Results

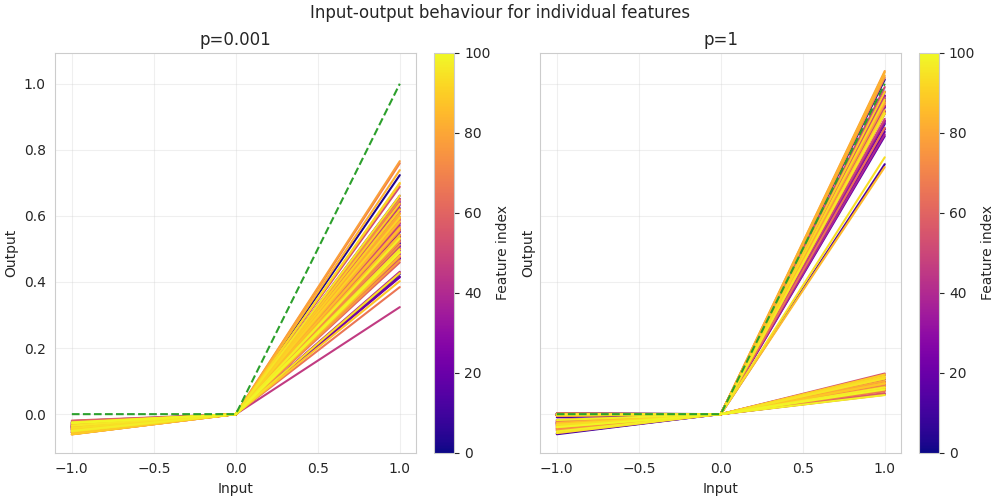
(06:37) Qualitatively different solutions in sparse vs. dense input regimes

(09:49) Quantitative analysis of the Compressed Computation model

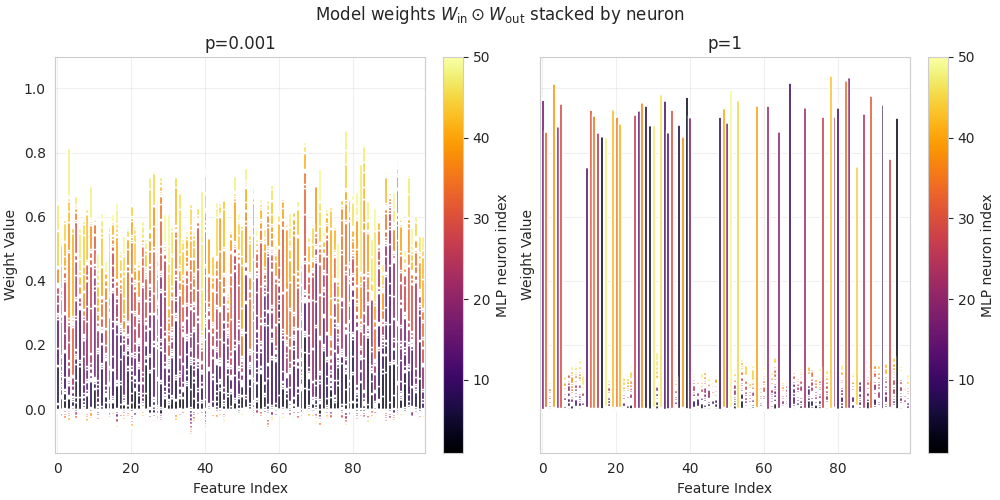
(13:09) Mechanism of the Compressed Computation model

(18:11) Mechanism of the dense solution

(20:55) Discussion

The original text contained 9 footnotes which were omitted from this narration.

---

First published:
June 23rd, 2025

Source:
https://www.lesswrong.com/posts/ZxFchCFJFcgysYsT9/compressed-computation-is-probably-not-computation-in

---

Narrated by TYPE III AUDIO.

---

Images from the article:

Figure 1: The original model architecture from Braun et al. (2025), and our simpler equivalent model.
Figure 2: Loss per feature (<span>__T3A_INLINE_LATEX_PLACEHOLDER___L/p___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>) as a function of evaluation sparsity. Each solid line corresponds to a model trained at a given sparsity. The models learn one of two solution types, depending on the input sparsity used during training: the “compressed computation” (CC) solution (violet) or a dense solution (green). Both types beat the naive baseline (dashed line) in their respective regime. Black circles connected by a dotted line represent the results seen by Braun et al. (2025), where models were evaluated only at their training sparsity.
Figure 3: Input/output behaviour of the two model types (for one-hot inputs): In the “compressed computation” solution (left panel), all features are similarly-well represented: each input activates the corresponding output feature. In contrast, the dense solution (right panel) shows a strong (and more accurate) response for half the features, while barely responding to the other half. The green dashed line indicates the expected response under perfect performance.
Figure 4: Weights representing each input feature, split by neuron. Each bar corresponds to a feature (x-axis) and shows the adjusted weight value from <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\text{out}} \odot W_{\text{in}}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>, split by neuron index (color). The CC solution (left) combinations of neurons to represent each feature (to around 70%), whereas the dense solution (right) allocates a single neuron to fully (~100%) represent 50 out of 100 features.
Figure 5, left: Loss per feature as a function of input sparsity, for different choices of <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>. We compare an embedding-like <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> (Braun et al. 2025, blue) to a fully random <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> (green) and a symmetric <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> (red) which is a random lower diagonal matrix mirrored; in both cases we set the magnitude if <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> that leads to the lowest loss. For comparison we also show a model trained on <span>__T3A_INLINE_LATEX_PLACEHOLDER___M=0___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> (yellow). We find that all non-zero <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> lead to a qualitatively similar profile, and that a symmetrized random <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> almost gives the same result as Braun et al. (2025).Right: Optimal loss as a function of mixing matrix magnitude <span>__T3A_INLINE_LATEX_PLACEHOLDER___\sigma___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> (separately trained for every <span>__T3A_INLINE_LATEX_PLACEHOLDER___\sigma___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>). For small <span>__T3A_INLINE_LATEX_PLACEHOLDER___\sigma___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> the loss linearly decreases with the mixing matrix magnitude, suggesting the loss advantage over the naive solution stems from the mixing matrix <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>. At large values of <span>__T3A_INLINE_LATEX_PLACEHOLDER___\sigma___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>, the loss increases again.
Figure 6: Training a model on the noisy dataset (<span>__T3A_INLINE_LATEX_PLACEHOLDER___M \neq 0___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>), and then fine-tuning on the clean <span>__T3A_INLINE_LATEX_PLACEHOLDER___M=0___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> case. We see that the loss jumps back up as soon as we switch to the clean task. This is evidence against the hypothesis that the CC solution wasn't learned on the clean case just due to training dynamics.
Figure 7, left: Cosine similarity between various eigen- and singular vectors (x-axis) and MLP neuron directions (y-axis). We show eigenvectors in the top panels, singular vectors in the bottom panels, the <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm in}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> matrix in the left panels, and the <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm out}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> matrix in the right panels. In all cases we see that the top-50 vectors (sorted by eigen- / singular value) have significant dot product with the neurons, while the remaining 50 vectors have near-zero dot products (black).Right: We test how well the ReLU-free MLP (i.e. just the <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm out} W_{\rm in}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> projection) preserves various eigen- (orange) and singular (blue) directions. Confirming the previous result, we find the cosine similarity between the vectors before and after the projection to be high for only the top 50 vectors.
Figure 8, left: Scatter plot of the entries of the product <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm out} W_{\rm in}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> and the mixing matrix <span>__T3A_INLINE_LATEX_PLACEHOLDER___M___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>; the entries are clearly correlated. The diagonal entries of <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm out} W_{\rm in}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> are offset by a constant, and seem to be correlated at a higher slope.Right: Visualization of the MLP weight matrices <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm in}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> and <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm out}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>. We highlight that <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm in}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> is has mostly positive entries (this makes sense as it feeds into the ReLU), and both matrices have a small number of large entries.
Figure 9: Loss of the SNMF solution, compared to the naive solution. Like in Figure 5b, the solution does better than the naive loss for a range of <span>__T3A_INLINE_LATEX_PLACEHOLDER___\sigma___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> values though the range is smaller and the loss is higher than for the trained model.
Figure 10, left: A non-zero offset in the <span>__T3A_INLINE_LATEX_PLACEHOLDER___W_{\rm out}___T3A_INLINE_LATEX_END_PLACEHOLDER__</span> entries of unrepresented features improves the loss in the dense regime. We determine the optimal value empirically for each input feature probability <span>__T3A_INLINE_LATEX_PLACEHOLDER___p___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>.Right: This hand-coded naive + offset model (dashed lines) consistently matches or outperforms the model trained on clean labels (solid lines) in the dense regime. (Note that this plot only shows the clean dataset (<span>__T3A_INLINE_LATEX_PLACEHOLDER___M=0___T3A_INLINE_LATEX_END_PLACEHOLDER__</span>) which is why no solution outperforms the naive loss in the sparse regime.)

Apple Podcasts and Spotify do not show images in the episode description. Try Pocket Casts, or another podcast app.

Senaste avsnitt

“against that one rationalist mashal about japanese fifth-columnists” by Fraser

13 juli | 6 min

“Surprises and learnings from almost two months of Leo Panickssery” by Nina Panickssery

13 juli | 12 min

“Vitalik’s Response to AI 2027” by Daniel Kokotajlo

12 juli | 24 min

“the jackpot age” by thiccythot

12 juli | 13 min

“Measuring the Impact of Early-2025 AI on Experienced Open-Source Developer Productivity” by habryka

11 juli | 12 min
Vad är en podd?

En liten tjänst av I'm With Friends. Finns även på engelska.

Podcastbild

00:00 -00:00
00:00 -00:00